単純に、無符号整数、すなわち正の整数のみを考えると、 8bitの2進数により表現できる数値の範囲は000000002から 111111112までとなるので、 これを10進数に置き換えると、010から25510となり、 8bitの情報量で表現可能な情報の種類の個数である、 256個の数値を表現することができる。
次に、有符号整数、すなわち正負の整数を考える。 有符号整数を8bitで表現する場合、演算上の便宜さから、 1bitを正もしくは0の場合に0、負の場合には1のように正負の符号の表現に使用し、 残りの7bitにより、 0および正の整数は無符号整数と同様に表現し、 負の整数は2の補数表現により定義することが多い。 2の補数表現とは、利用可能なビットに1ビットを加え、 最上位ビットを1、残りを0とした2進数から、 絶対値を減じた値により表現するものである。 例えば、-310を2の補数表現により7bitで表現する場合、 8bitの100000002から310を減じた、 11111002として表現する。
この場合、表現される整数の範囲は、表1に示すように -12810から12710となり、 その個数は、無符号整数と同様に256個となる。
| 10進数 | 2進数 |
|---|---|
| 127 | 01111111 |
| ... | ... |
| 2 | 00000010 |
| 1 | 00000001 |
| 0 | 00000000 |
| -1 | 11111111 |
| -2 | 11111110 |
| ... | ... |
| -128 | 10000000 |
浮動小数点数
2進数による実数の表現方法として、
小数点の位置を固定した表現による固定小数点数と、
小数点の位置を固定しない浮動小数点数の2種類がある。
固定小数点数では、小数点位置が固定されてしまうため、
大きな実数や小さな実数を表現できないという欠点があるため、
一般に、多くのコンピュータでは浮動小数点数が利用されている。
浮動小数点数による実数の表現は、
符号、指数部、および仮数部からなる。
すなわち、符号をs、指数をe、仮数をvとした場合、
例えば、以下のように実数rを表現することができる。
r = -1s × v × 2e
具体的には、8bitで浮動小数点数を表現する場合、
1bitで符号を表現し、3bitで有符号整数による指数を表現し、
残りの4bitで無符号整数による仮数を表現することができる。
例えば、実数3.2510は、
13×2-210と考えることができるので、
符号は02、指数部は1102、
仮数部は11012となり、
8bit全体では、表2に示すようになる。
表2: 8bit浮動小数点数の例
符号
指数部
仮数部
+
-2
13
0
1 1 0
1 1 0 1
この場合、表現できる数値の範囲として、
絶対値が0より大きい最も小さい値が1×2-4=0.062510 、
最も大きい値が15×23=12010となる。
なお、浮動小数点数を8bitにより表現することは一般的ではなく、
通常は、16bitや32bitにより表現されることが多い。
また、指数部、仮数部のビット数の取り方もシステムにより異なり、
仮数部の扱いも異なるため、
全体のビット数が同じであっても
表現できる数値の範囲や精度に違いがあることに注意すること。
ただし、表現できる実数の個数は256で変わらない。
□ アナログ信号のデジタル化
標本化と量子化
音声や映像など、連続的に変化する信号(アナログ信号)を
コンピュータで扱うためには、
離散的な信号(デジタル信号)に変換する必要がある。
これを一般にアナログ/デジタル変換(A/D変換)と呼び、
標本化と量子化により実現される。
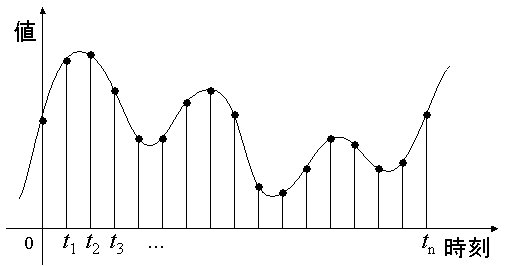
標本化とは、図1に示すように、
時間的に変化する信号を離散的に(多くは一定間隔で)観測し、
そのときの信号の大きさを測定(サンプリング)するものである。
測定された各信号の値を標本値と呼ぶ。
図1: アナログ信号の標本化
一般に、時間的に変化する信号は、
様々な周波数の正弦波の重ね合わせ
(フーリエ級数)からなっている。
このとき、その周波数の最大値の2倍の周波数でサンプリングを行えば、
このデータに基づき、もとの信号を再現できることが知られている
(標本化定理)。
信号を標本化しただけでは、各標本値はまだアナログデータであり、
コンピュータ等で扱うことはできない。
そのため、各標本値の量子化を行う。
量子化とは、得られたアナログ値をある一定の情報量で表現可能な値に
近似することである。
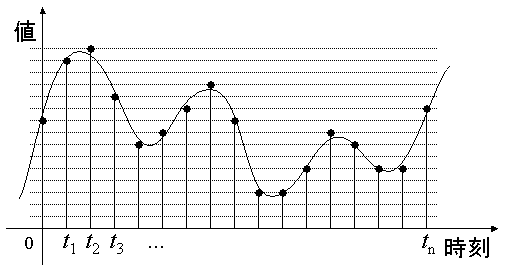
例えば、図2は、図1で示した標本値を4bit、16段階で量子化する例である。
図2: 標本化信号の量子化
量子化を行った場合、その値はもとの標本値とは異なる値となる。
例えば、信号の最大値を1とし、
これを四捨五入による近似によりn[bit]のデータに量子化を行った場合、
最大で、
1
(2n - 1)・2
の誤差が生じることになる。
すなわち、各標本値を示すデータのビット数を増やせば、
それだけもとの標本値に近い値とすることができるが、
どれだけビット数を増やしても、必ず誤差が生じることとなる。
ちなみに、CDに記録された音声は、
44KHzのサンプリングレート(標本化周波数)で、
16bit、65536段階を等間隔(線形: リニア)に
量子化を行ったデータとなっている(16bitリニアPCM:
Linear Pulse Code Modulation)。
量子化による誤差は多少あるが、
人の可聴領域は20Hz〜20KHz程度と言われており、
その意味では、最大周波数の倍である40KHzより大きな44KHzでの標本化は、
音声信号を記録するのに十分なデータ量であることがわかる。
データ量の圧縮
アナログ信号をデジタル信号に変換した場合、
単純な変換では、そのデータ量は膨大な量になる。
例えばCDの場合、3分程度の楽曲データであれば、
約15Mbyteのデータ量となる。
このような大きなデータを扱うのは大変である。
しかしながら、このようなアナログ信号をデジタル化したデータは、
多くの冗長性を含んでいる(不必要な情報を含んでいる)ことが多い。
例えば、一般的なアナログ信号は、
急激な変化がほとんどない(最大値から次の瞬間に0になったり、
0から最大値になったりしない)ことがわかっているため、
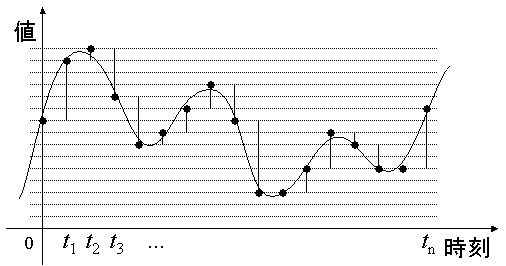
図3のように、前の値からの差分を取ることで、
表現する必要のある値の範囲を小さくすることができる
(ADPCM: Adaptive Differential PCM)。
リニアPCMの代わりにADPCMを利用した場合、
リニアPCMで16bitで表現された同じデータを12bit程度で表現できることが
知られている。
図3: 差分によるデジタル変換(ADPCM)
音声や画像など、特定のデータの場合、
人の聴覚や視覚の特性を利用したデータ圧縮方法も多い。
例えば、人の聴覚では、大きな音と小さな音がなっていた場合に、
たとえ両方の音が聞こえたとしても、小さな音はほとんど認識されない。
大きな振幅の周波数成分と小さな振幅の周波数成分がある場合、
小さな振幅の周波数成分を捨ててしまっても、
これを聴いた人はその違いがわからない。
そこで、音の周波数解析(離散コサイン変換: 一種のデジタルフーリエ変換)を行い、
不必要な周波数成分を削除することで、
データ量を減らすことができる。
MP3や、MDのデータ記録方式であるATRACは、
このような方法でデータ量の削減を行っている。
また、この方式を画像に適応したものが、JPEGである。
ただし、この場合、もとのアナログ信号とは
大きく異なる信号となることは明らかであり、
例えば、音声データの場合、
よく聴くと「音に厚みがない」などといった違いが感じられる。
■ レポート課題
□ レポート課題1
問1
16bitおよび32bitの2の補数表現により表現可能な有符号整数の範囲は、
それぞれどこからどこまでか。
問2
符号1bit、有符号整数による指数部7bit、無符号整数による仮数部8bitからなる、
16bitによる浮動小数点数を定義する。
この浮動小数点数により表現可能な実数の範囲として、
絶対値が0より大きい最も小さい値、および最も大きい値はそれぞれいくらか。
ただし、答えは、1.23×103のように、
有効数字3桁の10の指数表記で示すこと。
□ レポート課題2
問1
一般に、音声信号のようなアナログ信号は、
0V(ボルト)から5Vの電圧の変化による電気信号として入力され、
これをデジタル変換する。
0Vから5Vの電気信号を8bitおよび16bit無符号整数で線形に量子化した場合、
誤差の最大値はそれぞれ何Vになるか。
問2
1分間の音声データをサンプリングレート44KHz、16bitでデジタル化した場合、
そのデータ量は何Byteになるか。
■ 参考書籍、Web
-
瀧 保夫:「情報論I -情報伝送の理論-」, 岩波書店,
ISBN4-00-021236-2, 1,750円
Last modified: Thu Jun 12 21:40:00 JST 2003
| r = -1s × v × 2e |
| 符号 | 指数部 | 仮数部 |
|---|---|---|
| + | -2 | 13 |
| 0 | 1 1 0 | 1 1 0 1 |
標本化とは、図1に示すように、 時間的に変化する信号を離散的に(多くは一定間隔で)観測し、 そのときの信号の大きさを測定(サンプリング)するものである。 測定された各信号の値を標本値と呼ぶ。
 |
一般に、時間的に変化する信号は、 様々な周波数の正弦波の重ね合わせ (フーリエ級数)からなっている。 このとき、その周波数の最大値の2倍の周波数でサンプリングを行えば、 このデータに基づき、もとの信号を再現できることが知られている (標本化定理)。
信号を標本化しただけでは、各標本値はまだアナログデータであり、 コンピュータ等で扱うことはできない。 そのため、各標本値の量子化を行う。 量子化とは、得られたアナログ値をある一定の情報量で表現可能な値に 近似することである。 例えば、図2は、図1で示した標本値を4bit、16段階で量子化する例である。
 |
量子化を行った場合、その値はもとの標本値とは異なる値となる。 例えば、信号の最大値を1とし、 これを四捨五入による近似によりn[bit]のデータに量子化を行った場合、 最大で、
| 1 | ||
|
|
||
| (2n - 1)・2 | ||
の誤差が生じることになる。 すなわち、各標本値を示すデータのビット数を増やせば、 それだけもとの標本値に近い値とすることができるが、 どれだけビット数を増やしても、必ず誤差が生じることとなる。
ちなみに、CDに記録された音声は、 44KHzのサンプリングレート(標本化周波数)で、 16bit、65536段階を等間隔(線形: リニア)に 量子化を行ったデータとなっている(16bitリニアPCM: Linear Pulse Code Modulation)。 量子化による誤差は多少あるが、 人の可聴領域は20Hz〜20KHz程度と言われており、 その意味では、最大周波数の倍である40KHzより大きな44KHzでの標本化は、 音声信号を記録するのに十分なデータ量であることがわかる。
データ量の圧縮
アナログ信号をデジタル信号に変換した場合、
単純な変換では、そのデータ量は膨大な量になる。
例えばCDの場合、3分程度の楽曲データであれば、
約15Mbyteのデータ量となる。
このような大きなデータを扱うのは大変である。
しかしながら、このようなアナログ信号をデジタル化したデータは、
多くの冗長性を含んでいる(不必要な情報を含んでいる)ことが多い。
例えば、一般的なアナログ信号は、
急激な変化がほとんどない(最大値から次の瞬間に0になったり、
0から最大値になったりしない)ことがわかっているため、
図3のように、前の値からの差分を取ることで、
表現する必要のある値の範囲を小さくすることができる
(ADPCM: Adaptive Differential PCM)。
リニアPCMの代わりにADPCMを利用した場合、
リニアPCMで16bitで表現された同じデータを12bit程度で表現できることが
知られている。
図3: 差分によるデジタル変換(ADPCM)

音声や画像など、特定のデータの場合、
人の聴覚や視覚の特性を利用したデータ圧縮方法も多い。
例えば、人の聴覚では、大きな音と小さな音がなっていた場合に、
たとえ両方の音が聞こえたとしても、小さな音はほとんど認識されない。
大きな振幅の周波数成分と小さな振幅の周波数成分がある場合、
小さな振幅の周波数成分を捨ててしまっても、
これを聴いた人はその違いがわからない。
そこで、音の周波数解析(離散コサイン変換: 一種のデジタルフーリエ変換)を行い、
不必要な周波数成分を削除することで、
データ量を減らすことができる。
MP3や、MDのデータ記録方式であるATRACは、
このような方法でデータ量の削減を行っている。
また、この方式を画像に適応したものが、JPEGである。
ただし、この場合、もとのアナログ信号とは
大きく異なる信号となることは明らかであり、
例えば、音声データの場合、
よく聴くと「音に厚みがない」などといった違いが感じられる。
■ レポート課題
□ レポート課題1
問1
16bitおよび32bitの2の補数表現により表現可能な有符号整数の範囲は、
それぞれどこからどこまでか。
問2
符号1bit、有符号整数による指数部7bit、無符号整数による仮数部8bitからなる、
16bitによる浮動小数点数を定義する。
この浮動小数点数により表現可能な実数の範囲として、
絶対値が0より大きい最も小さい値、および最も大きい値はそれぞれいくらか。
ただし、答えは、1.23×103のように、
有効数字3桁の10の指数表記で示すこと。
□ レポート課題2
問1
一般に、音声信号のようなアナログ信号は、
0V(ボルト)から5Vの電圧の変化による電気信号として入力され、
これをデジタル変換する。
0Vから5Vの電気信号を8bitおよび16bit無符号整数で線形に量子化した場合、
誤差の最大値はそれぞれ何Vになるか。
問2
1分間の音声データをサンプリングレート44KHz、16bitでデジタル化した場合、
そのデータ量は何Byteになるか。
■ 参考書籍、Web
-
瀧 保夫:「情報論I -情報伝送の理論-」, 岩波書店,
ISBN4-00-021236-2, 1,750円
Last modified: Thu Jun 12 21:40:00 JST 2003
 |