2003年度前期 IT教育基礎論特論B
第7回: アルゴリズムとデータ構造
■ 概要
アルゴリズムとデータ構造の基礎を学習するとともに、
手続き型プログラミングパラダイムにおける
代表的なアルゴリズムを例にとり、
そのアルゴリズムとデータ構造を理解し、
プログラムの記述を行なう。
■ 目標
- アルゴリズムとデータ構造の概要の理解
- 代表的なアルゴリズムとデータ構造の理解
■ 目次
アルゴリズムとは、何らかの問題を解決したり、計算を行なうための手法を
自明な演算や手続きの組み合わせにより定義し、
文字や記号、数式等を用いて矛盾やあいまい性なく表現したものである。
一般に、手続き型プログラミングパラダイムにおける基本的なアルゴリズムは、
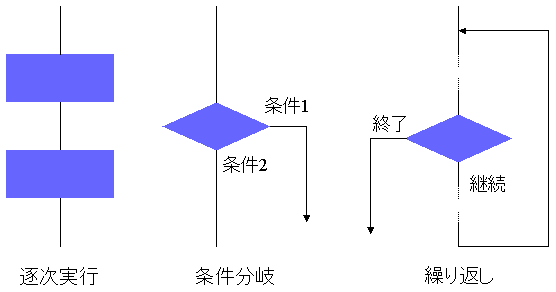
図1に示すように逐次実行、条件分岐、繰り返しの
3種類のアルゴリズムの組み合わせにより表現される。
図1: 基本アルゴリズム
 |
例えば、数値データの列(配列、リスト)があり、
この中から最大値を探し出すためのアルゴリズムは、
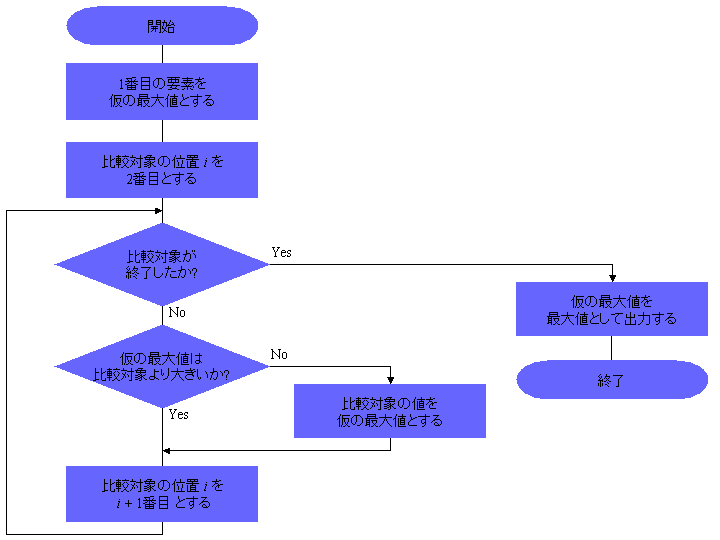
図2に示すようなフローチャートにより定義することができる
(アルゴリズムを表現するのに、フォローチャートを利用することも多いが、
必ずしもフローチャートによる必要はない)。
図2: 最大値を求めるアルゴリズム
 |
データ構造とは、なんらかの複数のデータを扱うために、
そのデータ群を格納するための構造のことである。
例えば、複数の同種のデータが存在し、それぞれのデータが独立している場合、
そのデータを1列に並べ、番号を付けておくと便利である。
この場合、図3に示すような、番号付けされた1列のデータ格納領域である
1次元配列などを利用するとよい。
図3: 配列
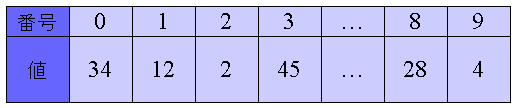 |
(注) コンピュータで配列を扱う場合、
配列の番号(添え字)が0から始まる事が多いため、
以下、配列の先頭の番号は図3のように0とし、これを0番目と呼ぶこととする。
データ構造は、どのようなデータをどのようなアルゴリズムにより
どのように処理するかに応じて、適切に定義する必要がある。
何らかの問題を解決するために、どのような処理を行なうか、
そのためのアルゴリズムが決まり、
また、データをどのように扱うか、
そのためのデータ構造が決まれば、
これに基づき、プログラムを記述することができる。
すなわち、アルゴリズムとデータ構造が決まれば、
プログラムはほぼ完成したものと言える。
逆に、アルゴリズムやデータ構造の定義があいまいであったり、
矛盾があったりすると、正しくプログラムを記述することはできない。
ただしくプログラムを記述するためには、
矛盾やあいまい性なく、アルゴリズムとデータ構造を定義する必要がある。
ただし、プログラミングパラダイムや言語仕様によって提供される基本機能や
定義できるデータ構造は異なるため、
解決しようとする問題や処理しようとする内容に応じて
適切なプログラミング言語を設定し、
その枠組みの中でアルゴリズムとデータ構造を考える必要がある。
繰り返し処理のある何らかのアルゴリズムにおいて、
その繰り返し処理中の主要な処理が何回繰り返されるかを計算量と呼ぶ。
例えば、図2で示した、数値データの列の中から最大値を求めるアルゴリズムでは、
2つの数値の比較を順番に繰り返すことによって最大値を決定するため、
n 個の数値データがあった場合には、n - 1回の比較が必要となる。
従って、このアルゴリズムの計算量は、
n 個のデータの場合にn - 1であると言うことができる。
計算量がan2 + bn + c のような
n の多項式で表現される場合、
n が大きくなると、最も次数の高い項がその式の形を特徴づけ、
それ以外の項は無視することができる。
そこで、計算量を示す多項式の最も次数の高い項から係数を除いたものを
オーダとよび、O (X )と書く
(X の部分にオーダを記述する)。
例えば、計算量がan2 + bn + c のオーダは
n2であり、O (n2 )と書く。
また図2の最大値を求めるアルゴリズムのオーダはn であり、
O (n )と書く。
なんらかの不規則に並んだデータ群を
ある基準に基づき順番に並べ変えることをソートするという。
ソートのアルゴリズムには多数の方法が提案されているが、
ここでは、簡単なソートのアルゴリズムとして
セレクションソートを紹介する。
例えば0番からn - 1番目までの配列に格納されたn 個の数値データを
セレクションソートにより大きい順に並べ替える場合を考える。
この場合先ず、ソートの対象範囲を全体、
すなわち0番目からn - 1番目までとし、
配列に格納された数値データ群の中から最大値を求めるアルゴリズムを応用し、
最大値が格納されている位置を求め、その値と、0番目の値とを交換する。
これにより、配列の先頭が最大値となるので、
次に、ソートの対象を1番目からn - 2番目までとし、
同様に最大値の位置を求め、1番目の値と交換する。
以上のような手続きをi 回繰り返すことにより
0番目からi - 1番目までが大きい順に並べられた状態となり、
i 番目からn - 1番目までを
次のソート対象範囲とすることができ、
対象範囲の要素数が1となったらソートを終了する。
以下のプログラムを作成し、実行結果を示せ。
ただし、プログラミング言語の種類は問わない。
数値データが格納された配列から最大値を求めるアルゴリズムに基づき、
n個の数値データが格納された配列に対し、
その配列とデータの個数を引数として与えると、
最大値が格納されている位置を求める手続き(関数)
select_max_point(array, n)を定義し、
この関数を利用して与えられた配列から最大値を求めるプログラムを作成せよ。
また、10個のデータ{1, 8, 3, 6, 5, 4, 7, 2, 9, 0}から最大値を求めた結果を示せ。
セレクションソートのアルゴリズムに基づき、
n個の数値データが格納された配列と
その配列に格納されたデータの個数を引数として与えると、
その配列の内容を大きい順に並べ替える手続き(関数)
selection_sort(array, n)を定義し、
この関数を利用して与えられた配列を大きい順に並べ替えるプログラムを作成せよ。
また、10個のデータ{1, 8, 3, 6, 5, 4, 7, 2, 9, 0}をソートした結果を示せ。
ソートのアルゴリズムの1つに、マージソートがある。
マージソートのアルゴリズムについて調べ、
8個のデータ{1, 8, 3, 6, 5, 4, 7, 2}をマージソートにより
ソートする際の手順を図示せよ。
セレクションソートおよびマージソートに対して、データ間の比較に着目し、
n 個のデータのソートにかかる計算量およびオーダをそれぞれ求め、
ソートの効率について比較、考察せよ。
なお、n は
n = 2k (k は整数)であるような値と仮定してよい。
ただし、計算量を示す式にk があってはいけない。
-
Alan W. Biermann 著, 和田 英一 監訳:
「やさしいコンピュータ科学」, アスキー,
ISBN4-7561-0158, 4660円
Last modified: Sun Jun 01 22:24:27 JST 2003



