2004年度前期 IT教育基礎論特論B
情報とデータとの関係を理解するとともに、 データ化された情報の情報量の算出方法を学習する。
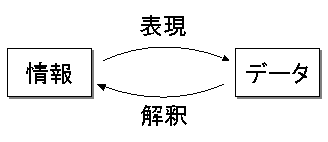
情報とは、知識や技術などのように人の頭の中や、 なんらかの事象の中にあるものである。 この情報を相手伝達するには、 これを言葉や文字、記号、動作などの何らかの形で表現する必要がある。 この情報を表現したものを「符号」 もしくは「データ」と呼ぶ。 また、伝達されたデータを情報として得るには、 受け取った符号を人が解釈する必要がある。 すなわち、情報とデータとは、図1に示す関係にあるといえる。
 |
情報量とは、情報源から何らかのデータを受け取った際に、 これにより知ることのできる情報の量を示すものである。 最も単純な情報は、○か×か、白か黒か、明日晴れるか否か、 のように2種類の情報があり、データを受け取ることにより、 そのどちらであるかが判る場合である。
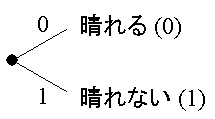
このように、情報源から得られる情報に2種類の状態がある場合、 図2に示すように、どちらか一方を0、もう一方を1とした、 2進数で1桁のデータとして表現することができる。 これを情報量の単位として「1bit」と定義する。 すなわち、明日、晴れるかどうかわからない場合に、 天気予報で明日の天気が晴れである、もしくは晴れないことを知った場合、 1bitの情報量を得ることになる。
 |
2種類の状態からなる情報の情報量は1bitであることがわかった。 次に、2種類以上の状態からなる情報の情報量を考える。
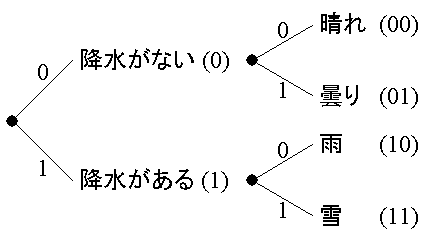
例えば、明日の天気として、晴れ、曇り、雨、雪の4種類があり、 どれも同じ確率で、どれになるか全くわからないとする。 この場合、図3に示すように、 先ず、降水がない場合と降水がある場合とで、 それぞれ(晴れ, 曇り)と(雨, 雪)の2種類の状態に分け、 次に、降水がない場合を晴れと曇りに、 また降水がある場合を雨と雪に分けて考えることができ、 2進数で2桁の数値により表現することができる。
 |
すなわち、晴れ、曇り、雨、雪のように 4種類の状態のある情報源から1つの情報を得る場合、 2進数で2桁の数値により表現できる情報を得ることとなり、 その情報量は2bitとなる。
上記例では、晴れ、曇り、雨、雪のそれぞれが同じ確率で起こる場合を考えたが、 実際には、それぞれの生起確率が異なり、予め判っている場合も多い。 この場合、たいてい起こるであろうことを知っても、その情報量は小さく、 また、めったに起こらないことを知った場合には、 情報量が大きいと考えるほうが自然である。
例えば、ある季節の天気は、 晴れの確率が50%、曇りの確率が25%、雨および雪の確率が それぞれ12.5%と判っているとする。 この場合、晴れるか晴れないか、すなわち晴れとそれ以外の確率が等しいので、 晴れの情報量とそれ以外の情報量が等しいと考えることができる。 また、晴れではない場合に、降水があるかないか、 すなわち曇りとそれ以外の確率が等しいので、 曇りの情報量と雨もしくは雪である情報量が等しいと考えることができる。
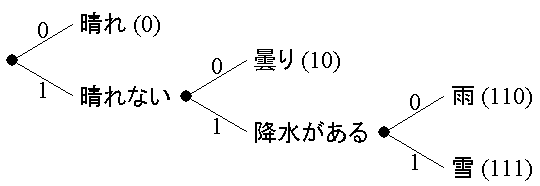
このように考えると、先ず、晴れとそれ以外の状態(曇り, 雨, 雪)に分け、 次に、曇りとそれ以外の状態(雨, 雪)に分け、さらに雨と雪に分け、 図4に示すように符号化することができ、 晴れは1bit、曇りは2bit、雨および雪は3bitとなる。
 |
以上のような理論に基づき、ある事象aがあり、 その生起確率がP (a )である場合、 その情報量I (a )を 事象aの自己情報量(self-information)と呼び、 以下のように定義する。
| I (a ) = log2 | 1 | [bit] |
|
|
||
| P (a ) |
なお、情報科学の分野では対数の底を2とすることが多いため、 以降特に断らない場合は、 log2の底を省略し、単にlogと記述する。
また、現在のコンピュータでは極めて大きな情報量を扱うため、 場合によってはbitを単位として情報量を表現していると不便なことが多い。 そこで、8bit(8b)をまとめて1Byte(1B)とする、Byteを単位として表記することも多い。 さらに多くの情報量を扱う場合、 1024Byteを1KByte、1024KByteを1MByteのように表記することも多い。 ただし、1KByteは1000Byteではないことに注意すること。
熱力学に置いて、ある状態の無秩序さを表現する方法としてエントロピーがある。 エントロピーとは、その状態が確定的であれば0であり、 無秩序であればあるほど大きな値となる。 情報においても、これと同様に情報源の不確定さを示す エントロピーを定義することができる。 情報源の不確定さとは、 その情報源からどの情報が得られるか判らない状態を示すものである。
ある情報源X から得られる全ての事象を {a1, a2, a3, ..., an }とし、 各事象ai (ただし、i = 1, 2, 3, ..., n)の生起確率がそれぞれ P (ai )であるとする。 このとき、情報源X から 1つの事象ai が得られた際に 得られる情報量I (ai )は 以下のようになる。
| I (ai ) = log | 1 |
|
|
|
| P (ai ) |
従って、各事象から得られる情報量の期待値(平均情報量) E[I (ai )]は、 以下のようになる。
| E[I (ai )] | = |
|
|||||||||
| = |
|
もし、2種類の事象 {a0, a1}からなる情報源X があり、 各事象の生起確率がそれぞれ P (a0) = p , P (a1) = 1 - p の場合、 その平均情報量 E[I (ai )]は、 以下のようになる。
| E[I (ai )] = -p logp - (1-p ) log(1-p ) |
これをp の値に応じてグラフ化すると、図5のようになる。
| 平 均 情 報 量 |
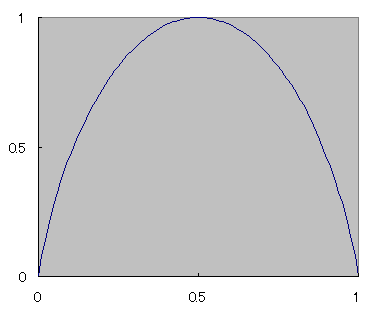 |
| 生起確率p | |
このグラフを見ると判るとおり、 2種類の事象の生起確率が同じ場合に(p = 1 - p = 0.5)に、 平均情報量がもっとも大きく、 逆に、生起確率に偏りがあるほど、平均情報量は小さい。 これは、2種類以上の事象の場合でも同様である。 このことは、どの事象が起こるか判らない、 情報源の状態が不確定である場合、そこから得られる平均情報量が大きく、 また、どの事象が起こるか予め予想がつく場合には、 平均情報量が小さいことを示している。
すなわち、情報源X の平均情報量の大きさは、 情報源X の不確定さを示しているといえる。 そこで、情報源X の平均情報量 E[I (ai )]を 情報源X のエントロピーと定義し、 以下のようにH (X )と書く。
| H (X ) = E[I (ai )] = - |
|
P (ai ) log P (ai ) |
情報源として、ある季節1の天気 X1={快晴, 晴れ, 曇り, 雨, 雪}、 およびこれとは別の季節2の天気 X2={快晴, 晴れ, 曇り, 雨, 雪}があるとする。 それぞれの生起確率は表3に示す通りとする。 これに基づき、以下の課題に答えよ。 ただし、計算結果の途中の式も示すこと。
| 快晴 | 晴れ | 曇り | 雨 | 雪 | ||
|---|---|---|---|---|---|---|
| 季節1 | 12.50 | 12.50 | 25.00 | 25.00 | 25.00 | |
| 季節2 | 25.00 | 50.00 | 12.50 | 12.50 | 0.00 |
季節1において、天気予報により翌日の天気が 「晴れ」であることが判った。 このとき得られる情報量は何[bit]か。
季節2において、天気予報により翌日の天気が 「晴れ」であることが判った。 このとき得られる情報量は何[bit]か。
季節1において、天気予報により翌日は雨にも雪にもならないことが判った。 このとき得られる情報量は何[bit]か。
季節1において、天気予報により翌日の天気は雨または雪になることが判っている。 その後、さらに天気予報により翌日の天気は雪になることが判った。 後の天気予報により得られる情報量は何[bit]か。
季節1の天気と、季節2の天気では、どちらがより不確定か。 両者のエントロピーの大きさを示し、答えよ。