 |
2004年度前期 IT教育基礎論特論B
アルゴリズムとデータ構造の基礎を学習するとともに、 手続き型プログラミングパラダイムにおける 代表的なアルゴリズムを例にとり、 そのアルゴリズムとデータ構造を理解し、 プログラムの記述を行なう。
アルゴリズムとは、何らかの問題を解決したり、計算を行なうための手法を 自明な演算や手続きの組み合わせにより定義し、 文字や記号、数式等を用いて矛盾やあいまい性なく表現したものである。
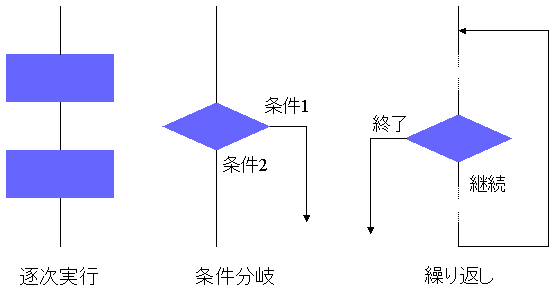
例えば、手続き型プログラミングパラダイムでは、 手続きの組み合わせによりアルゴリズムを定義し、表現することができる。 一般に、手続き型プログラミングパラダイムに基づくプログラムは、 図1に示すように逐次実行、条件分岐、繰り返しの 3種類の手続きからなることを学習した。 これらの手続きは、何らかの問題を解決する手続きであるため、 基本的なアルゴリズムであると考えると、 これらの組み合わせにより表現される
 |
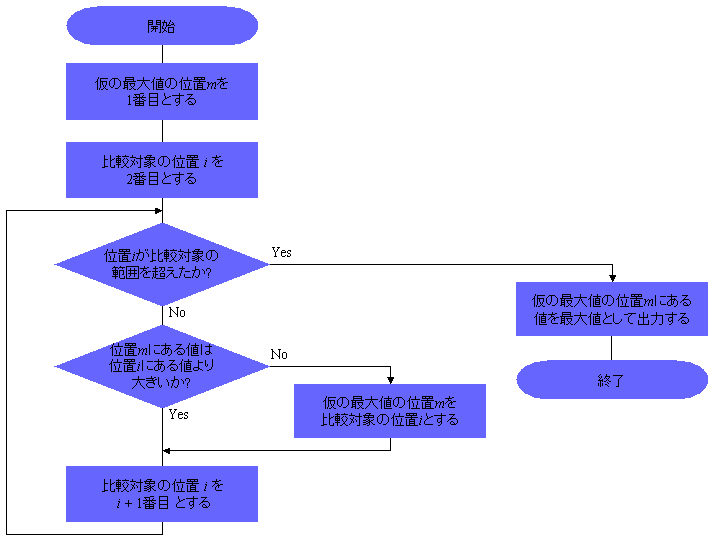
例えば、数値データの列(配列、リスト)があり、 この中から最大値を探し出すためのアルゴリズムは、 図2に示すようなフローチャートにより定義することができる (アルゴリズムを表現するのに、フォローチャートを利用することも多いが、 必ずしもフローチャートによる必要はない)。
 |
データ構造とは、なんらかの複数のデータを扱うために、 そのデータ群を格納するための構造のことである。
例えば、複数の同種のデータが存在し、それぞれのデータが独立している場合、 そのデータを1列に並べ、番号を付けておくと便利である。 この場合、図3に示すような、番号付けされた1列のデータ格納領域である 1次元配列などを利用するとよい。
|
(注) コンピュータで配列を扱う場合、 配列の番号(添え字)が0から始まる事が多いため、 以下、配列の先頭の番号は図3のように0とし、これを0番目と呼ぶこととする。
データ構造は、どのようなデータをどのようなアルゴリズムにより どのように処理するかに応じて、適切に定義する必要がある。
何らかの問題を解決するために、どのような処理を行なうか、 そのためのアルゴリズムが決まり、 また、データをどのように扱うか、 そのためのデータ構造が決まれば、 これに基づき、プログラムを記述することができる。 すなわち、アルゴリズムとデータ構造が決まれば、 プログラムはほぼ完成したものと言える。 このため、「アルゴリズム + データ構造 ≒ プログラム」と言われることも多い。 逆に、アルゴリズムやデータ構造の定義があいまいであったり、 矛盾があったりすると、正しくプログラムを記述することはできない。 正しくプログラムを記述するためには、 矛盾やあいまい性なく、アルゴリズムとデータ構造を定義する必要がある。
ただし、プログラミングパラダイムや言語仕様によって提供される基本機能や 定義できるデータ構造は異なるため、 解決しようとする問題や処理しようとする内容に応じて 適切なプログラミング言語を設定し、 その枠組みの中でアルゴリズムとデータ構造を考える必要がある。 また、実際のプログラムを作成するためには、 そのプログラミング言語の仕様に基づき、 具体的なプログラムコードを記述する必要がある。 従って、「アルゴリズム + データ構造 ≒ プログラム」ではあるが、 実際には、アルゴリズムとデータ構造とプログラムの関係は、 図4のようになると言えよう。
|
|
|
|
|
|||||
先に、配列として定義されたデータ列から最大値を求めるアルゴリズムを紹介したが、 その他にも、様々な問題の解法としてのアルゴリズムが知られている。 ここでは、ソートアルゴリズムを紹介する。
ソートとは、 なんらかの不規則に並んだデータ群を ある基準に基づき順番に並べ変えることをいう。 ソートのアルゴリズムには多数の方法が提案されているが、 ここでは、簡単なソートのアルゴリズムとしてセレクションソート、 ならびに比較的効率の良いアルゴリズムとしてマージソートを紹介する。
例えば0番からn - 1番目までの配列に格納されたn 個の数値データを セレクションソートにより大きい順に並べ替える場合を考える。 この場合先ず、ソートの対象範囲を全体、 すなわち0番目からn - 1番目までとし、 配列に格納された数値データ群の中から最大値を求めるアルゴリズムを応用し、 最大値が格納されている位置が0番目と異なる場合には、 最大値が格納されている位置の値と0番目の値とを交換する。 これにより、配列の先頭が最大値となるので、 次に、ソートの対象を1番目からn - 2番目までとし、 同様に最大値の位置を求め、1番目の値と交換する。
以上のような手続きをi 回繰り返すことにより 0番目からi - 1番目までが大きい順に並べられた状態となり、 i 番目からn - 1番目までを 次のソート対象範囲とすることができ、 対象範囲の要素数が1となったらソートを終了する。
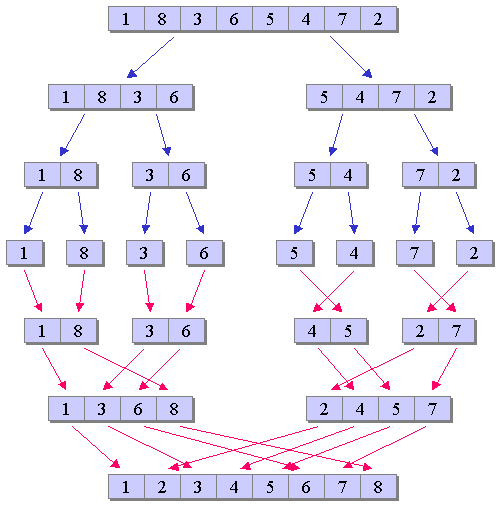
マージソートは、ソートアルゴリズムの1つとしてよく知られたアルゴリズムであり、 分割と統合により定義される。 クイックソート等に比べると効率性に欠ける場合もあるが、 データ列の並び方によらず安定した計算量に収まるといった特徴を持つ。 このマージソートのアルゴリズムは、 ある数列をマージソートによりソートする場合、 一般に、図1のように表される。
|
図1は極めて単純な図であり、 取り立てて複雑なことは行っていないため容易に実装できそうにも思える。 しかしながら実際にプログラムを記述する場合には、 気をつけなければいけない部分も少なくない。
先ず、分割と統合の処理手順に関して、 図1を見ると、先ず、全ての列が要素数1になるまで分割を繰り返し、 その後、統合を繰り返すというような、 上から下に処理が進めればよいように感じられるかもしれない。 しかしながら、マージソートにおける一般的な処理手順は 必ずしも上から下に進められるとは限らない。 マージソートのアルゴリズムは 関数の再帰呼び出しの例として取り上げられることも多く、 一般に、再帰的に以下のように定義することができる。
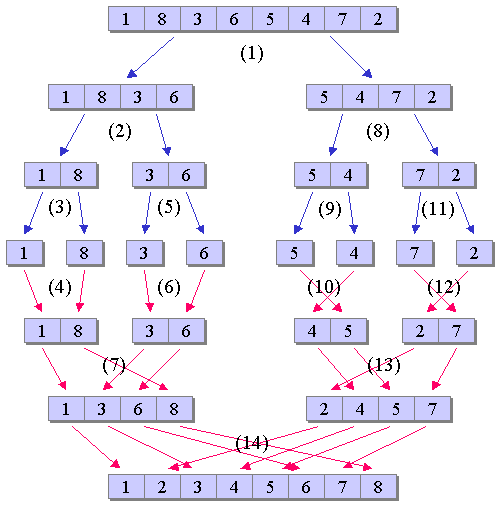
この時、3. の部分が再帰的な定義になっている。 この3.の部分の再帰呼び出しにおいて、 マルチスレッド等の特別な処理を行わず 一般的な逐次処理によりマージソートを行う場合、 例えば、前半部を先にマージソートによりソートし、 これが終了した後に後半部のマージソートを行う、 という形で処理手続きを定義すると、 実際には、前半部のマージソートを行うために、 さらにこれを前半部と後半部に分割し、 さらにまたこの前半部のマージソートを行うために... という具合に処理が進められることになる。 従って、図1のマージソートの例において、 分割、統合の処理に順番に番号をふると、図2のようになる。
|
この図をみるとわかるように、 マージソートによる分割、統合の処理は、 全てを分割した後に統合を行うのではなく、分割と統合を繰り返し、 図の上では、上と下を行きつ戻りつしていることが確認できる。 もし、これを勘違いして、先ず全てを分割しなければならないと思い込んでしまうと、 関数の再帰呼び出しによるプログラムの記述ができなくなってしまう。
配列を前半部と後半部に分割し、 2つの配列とするのにどのようにしたら良いだろうか? 図1では、もともとの数列を2つに分割する際に、 大きさが半分の2つの数列を新たに用意しているように見えるかもしれない。 実際、データ列を分割するたびに新たなデータ列を用意しても プログラムを記述することはできるが、 その場合、分割の段数分だけ新たにデータ列を用意することとなり、 もとのデータの何倍ものデータ格納領域が必要となる。 もし、大量のデータをマージソートによりソートする場合、 これは現実的な方法とはいえない。
これに対し、マージソートにおける分割は、 データ列の入れ替えを行うわけではなく、 処理対象となる範囲を指定しているだけであることに着目すると、 余計なデータ列を生成する必要がないことがわかる。 すなわち、マージソートの手続きを あるデータ列におけるソート範囲の始点と終点を指定するように定義すればよい。 すなわち、マージソートの処理手続きを以下のように定義することができる。
マージソートの処理手続きにおける、 3.の前半部と後半部の2つのデータ列の統合において、 その処理手続きは以下のように定義することができる。
これをそのままプログラムとして実装する方法もあるが、 その場合、統合の処理の度に、 統合済みのデータ列を格納するためデータ格納領域を新たに用意することとなり、 結果的に段数分だけ、新たなデータ格納領域を用意する必要があり、現実的ではない。
これに対し、前半部と後半部の統合のために、それぞれのデータ列を一時的に複製し、 もとのデータ列の格納領域を統合済みデータ列の格納領域として使用すれば、 統合が終了した時点で、 一時的に用意した複製を格納するためのデータ格納領域は使用済みとなり、 次の統合のために新たなデータ格納領域を用意する必要はない。 しかしながら、このような処理手続きの場合にも、 もとのデータ列の大きさと同じだけのデータ格納領域が必要となる。 また、前半部、後半部の統合において、比較による結合の結果残ったデータ列を 必ず統合済みデータ列に結合してやらなければならない。
ここで、2つのデータ列の統合においてデータを1つ1つ結合する度に、 未処理データから1つ1つデータを取り除くことに着目すると、 前半部のみを複製し、退避させてやれば良いことがわかる。 この場合、一時的に用意すべきデータ格納領域は もとのデータ列の半分の大きさで済むだけでなく、 後半部のデータの複製処理、 および比較によるデータ列の結合の結果として後半部のデータ列が残った場合の 未処理データの結合処理を行う必要がなく、 効率的なプログラムの実行が可能となり、大幅な実行速度の向上が見込まれる。
以上のマージソートのアルゴリズムに基づき、 実際に、標準入力から入力された数列を配列に格納し、 ソートするプログラムを記述すると以下のようになる。
/* merge-sort-number.c */
#include <stdio.h>
#define ARRAY_MAX 65536
/* ソート対象配列へのデータの読み込み関数 */
int input_data(int array[]) {
int i, d;
for( i = 0; i < ARRAY_MAX; i++ ) {
if ( scanf("%d", &d) == EOF ) {
return i;
} else {
array[i] = d;
}
}
fprintf(stderr, "Out of maximum amount(%d).", 65536);
return i;
}
/* マージソート関数 array[]: ソート対象配列, left: 左端, right: 右端 */
void merge_sort(int array[], int left, int right) {
int reserve[ARRAY_MAX / 2 + 1]; /* 前半部退避用の配列 */
int mid; /* 左端と右端の中間位置を示す変数 */
int i; /* 退避用配列の添え字のカウンタ */
int reserve_end; /* 退避用配列の右端 */
int j; /* ソート対象配列の後半部の添え字のカウンタ */
int k; /* ソート対象配列の添え字のカウンタ */
if ( left == right ) return; /* 配列の要素が空であれば何もせず戻る */
mid = (left + right) / 2; /* 配列の中間位置を求める */
merge_sort(array, left, mid); /* 再帰呼び出しにより前半部をソート */
merge_sort(array, mid + 1, right); /* 再帰呼び出しにより後半部をソート */
for( i = 0, k = left; k <= mid; i++, k++ ) { /* 前半部を退避 */
reserve[i] = array[k];
}
i = 0; /* 退避された前半部の比較位置の初期値を設定 */
j = mid + 1; /* 後半部の比較位置の初期値を設定 */
reserve_end = mid - left; /* 退避された前半部の右端を設定 */
k = left; /* マージした結果の格納位置の初期値を設定 */
/* 退避された前半部、および後半部が残っている間、マージ */
while( i <= reserve_end && j <= right ) {
if ( reserve[i] >= array[j] ) {
array[k] = reserve[i]; /* 退避された前半部からマージ */
i++;
} else {
array[k] = array[j]; /* 後半部からマージ */
j++;
}
k++; /* マージ位置を右に移動 */
}
/* 比較によるマージ後、退避された前半部が残っていれば無条件にマージ */
while( i <= reserve_end ) {
array[k] = reserve[i];
i++;
k++;
}
}
int main(int argc, char **argv) {
int array[ARRAY_MAX]; /* ソート対象配列の用意 */
int amount; /* ソート対象配列の要素数 */
int i;
amount = input_data(array); /* データ読み込み関数呼び出し */
merge_sort(array, 0, amount - 1); /* マージソート関数呼び出し */
for( i = 0; i < amount; i++ ) { /* 結果出力 */
printf("%d ", array[i] );
}
printf("\n");
}
|
このプログラムを実行すると、 以下のように正しくソートすることができることを確認できる。
./merge-sort-number 1 8 3 6 5 4 7 2 ここで、Ctrl-Dを入力する 8 7 6 5 4 3 2 1 |
繰り返し処理のある何らかのアルゴリズムにおいて、 その繰り返し処理中の主要な処理が何回繰り返されるかを計算量と呼ぶ。
例えば、図2で示した、数値データの列の中から最大値を求めるアルゴリズムでは、 2つの数値の比較を順番に繰り返すことによって最大値を決定するため、 n 個の数値データがあった場合には、n - 1回の比較が必要となる。 従って、このアルゴリズムの計算量は、 n 個のデータの場合にn - 1であると言うことができる。
計算量がan2 + bn + c のような n の多項式で表現される場合、 n が大きくなると、最も次数の高い項がその式の形を特徴づけ、 それ以外の項は無視することができる。 そこで、計算量を示す多項式の最も次数の高い項から係数を除いたものを オーダとよび、O (X )と書く (X の部分にオーダを記述する)。
例えば、計算量がan2 + bn + c のオーダは n2であり、O (n2 )と書く。 また図2の最大値を求めるアルゴリズムのオーダはn であり、 O (n )と書く。
数値データが格納された配列から最大値を求めるアルゴリズムに基づき、
n個の数値データが格納された配列に対し、
その配列とデータの個数を引数として与えると、
最大値が格納されている位置を求める手続き(関数)
select_max_point(array, n)を定義し、
この関数を利用して標準入力から入力された値を格納した配列から
最大値を求めるプログラムを作成せよ。
ただし、標準入力から入力されたデータの配列への取り込みは、
マージソートのプログラムを参考にせよ。
実行結果には、 10個のデータ{1, 8, 3, 6, 5, 4, 7, 2, 9, 0}から最大値を求めた結果を示せ。
(1)で作成した、n個の要素の中から最大値を求める関数を改良し、 m番目の要素からn番目の要素の中から最大値の位置を求める関数 select_max_point(array, m, n)を定義し、 この関数を利用して、 標準入力から入力された値を格納した配列のm番目からn番目の要素の中から 最大値を求めるプログラムを作成せよ。 ただし、ここでいうm番目とは、配列の添え字として0番目から始まることに注意せよ。
実行結果には、 10個のデータ{1, 8, 3, 6, 5, 4, 7, 2, 9, 0}のうち、 2番目から7番目の中の最大値を求めた結果を示せ。
セレクションソートのアルゴリズムに基づき、
n個の数値データが格納された配列と
その配列に格納されたデータの個数を引数として与えると、
その配列の内容を大きい順に並べ替える手続き(関数)
selection_sort(array, n)を定義し、
この関数を利用して与えられた配列を大きい順に並べ替えるプログラムを作成せよ。
なお、最大値の位置を求める手続きには、
(2)で定義した関数を利用するとよい(しなくてもよい)。
実行結果には、 10個のデータ{1, 8, 3, 6, 5, 4, 7, 2, 9, 0}をソートした結果を示せ。
セレクションソートおよびマージソートに対して、 データ間の比較回数(マージソートの場合は最小値と最大値)に着目し、 n 個のデータのソートにかかる計算量およびオーダをそれぞれ求め、 ソートの効率について比較、考察せよ。
なお、n は n = 2k (k は整数)である値と仮定してよい。 ただし、計算量を示す式にk があってはいけない。
以下のプログラムは、0から第1引数で指定された値の範囲で、 第2引数で指定された個数の乱数を出力するプログラムである。
/* create-random-numbers.c */
#include <stdio.h>
#include <stdlib.h>
/* 1970年からの経過秒を得るtime()関数を利用するためのインクルードファイル */
#include <sys/types.h>
#include <time.h>
void usage(char *command_name) {
printf("usage: %s
|
例えば、0から5までの範囲で10個の乱数を出力するには、 以下のように実行する。
$ ./create-random-numbers 5 10 0 3 2 2 0 0 2 2 5 2 $
このプログラムを使用して、0から100までの範囲で、 10個、20個、30個、...100個の10種類の乱数列を保存したファイルを それぞれ用意し、 各乱数列をセレクションソート、マージソートのそれぞれを利用して 並べ替えを行った際の比較回数に着目した計算量を計測し、 乱数列の要素数に対する計算量の実測値のグラフを作成し、 各ソートの計算量と一致することを確認せよ。
ただし、上記の乱数生成プログラムを使用して生成される 乱数列をファイルに保存する場合、 UNIXのリダイレクト機能を利用するとよい。 例えば、0から100までの範囲の50個の乱数を random-numbers-100というファイルに保存する場合、 以下のように実行する。
$ ./create-random-numbers 100 50 > random-numbers-50 $
また、計算量を測定するための比較回数のカウントは、 以下の様に、カウント用の変数をグローバル変数として用意し、 if文による比較を行う部分の前に変数の値に1を加え、 並べ替えが終了した後のプログラムの最後の部分で 変数の値を標準エラー出力に出力するよう、プログラムを修正するとよい。
/* merge-sort-number-2.c */
#include <stdio.h>
int counter=0; /* 比較回数カウント用グローバル変数の宣言と初期化 */
...
/* マージソート関数 array[]: ソート対象配列, left: 左端, right: 右端 */
void merge_sort(int array[], int left, int right) {
...
/* 退避された前半部、および後半部が残っている間、マージ */
while( i <= reserve_end && j <= right ) {
counter++; /* 比較回数のカウント */
if ( reserve[i] >= array[j] ) { /* ここが比較箇所 */
...
}
int main(int argc, char **argv) {
...
printf("\n");
/* プログラムの最後の部分で、計測数を標準エラー出力に出力 */
fprintf(stderr, "Number of comparisons is %d.\n", counter);
}
|
これにより、以下の様に ファイルに保存した乱数列をリダイレクトにより標準入力から読み込み、 また、標準出力を/dev/nullにリダイレクトすることにより、 ソート結果は画面には表示せず、 計測結果のみを得ることができる。
$ ./merge-sort-number < random-numbers-50 > /dev/null Number of comparisons is 221. $