2005年度前期 IT教育基礎論特論B

第5回: 知識の定義と推論(2)

概要と目標

■ 概要

コンピュータによる情報処理の基礎となっている命題論理、 およびこれを代数により表現するブール代数を理解する。

■ 目標

• 命題論理の理解
• ブール代数による表現手法の理解
• ブール代数の演算規則の理解

目次

• 講義内容
• はじめに
• ブール代数
• ブール代数とは
• ブール代数の定理
• 論理回路
• 論理ゲート
• 半加算器と全加算器
• レポート課題
• レポート課題1
• レポート課題2
• レポート課題3
• 参考書籍

講義内容

■ はじめに

コンピュータシステムは、様々な複雑な情報処理を行うことが可能であるが、 基本的には、極単純な論理回路を組み合わせることによりこれを実現している。 本講義では、コンピュータによる情報処理の仕組みを理解するために、 コンピュータを構成する論理回路の基礎である命題論理、 ならびにこの命題論理を代数の形で表現したブール代数について学習する。

■ ブール代数

□ ブール代数とは

ブール代数とは、集合Bの要素(一般にはB≡{0, 1})に対し、 表1の単項演算子NOT(     )、 二項演算子AND(・)、OR(+)による演算を行い、 結果として集合Bの要素を得る代数系である。 任意の要素X, Y, Z ∈ Bに対し、 表2に示す法則が成り立つ場合、これをブール代数と呼ぶ。 これは、命題論理における真偽をそれぞれ1および0とし、 また、否定、論理積、論理和の各論理記号を それぞれNOT、AND、ORの演算子に置き換えたものともいえる。

表1: ブール代数の演算子

演算子	意味	演算式の例
	NOT (negative)	X
・	AND (conjunction)	X ・Y
+	OR (disjunction)	X +Y

表2: ブール代数の演算式

交換律	X ・ Y = Y ・ X
	X + Y = Y + X
分配律	X ・ (Y + Z ) = (X ・ Y ) + (X ・ Z )
	X + (Y ・ Z ) = (X + Y ) ・ (X + Z )
同一律	X ・ 1 = X
	X + 0 = X
補元律	X ・ X = 0
	X + X = 1

□ ブール代数の定理

ブール代数の定義に基づき、様々な定理を導くことができる。 以下、その例を示す。

定理(1)

任意のX において、X ・ X = X ならびに X + X = X が成り立つ。

証明

X ・ X = (X ・ X ) + 0 :同一律 = (X ・ X ) + (X ・ X ) :補元律 = X ・ (X + X ) :分配律 = X ・ 1 :補元律 = X :同一律

X + X = (X + X ) ・ 1 :同一律 = (X + X ) ・ (X + X ) :補元律 = X + (X ・ X ) :分配律 = X + 0 :補元律 = X :同一律

定理(2)

任意のX において、X ・ 0 = 0 ならびに X + 1 = 1 が成り立つ。

証明

X ・ 0 = (X ・ 0) + 0 :同一律 = (X ・ 0) + (X ・ X ) :補元律 = X ・ (0 + X ) :分配律 = X ・ X :同一律 = 0 :補元律

X + 1 = (X + 1) ・ 1 :同一律 = (X + 1) ・ (X + X ) :補元律 = X + (1 ・ X ) :分配律 = X + X :同一律 = 1 :補元律

定理(3)

任意のX , Y において、 X ・ (X + Y ) = X + X ・ Y = X が成り立つ。

証明

X ・ (X + Y ) = (X + 0) ・ (X + Y ) :同一律 = X + (0 ・ Y ) :分配律 = X + 0 :定理(2) = X :同一律

X + (X ・ Y ) = (X ・ 1) + (X + Y ) :同一律 = X ・ (1 + Y ) :分配律 = X ・ 1 :定理(2) = X :同一律

■ 論理回路

命題の真偽やブール代数の1、0を電気信号のON、OFFとして入力し、 命題論理やブール代数に基づく論理演算を行なう電子回路を論理回路と呼ぶ。 論理回路では、論理演算の結果を同様に電気信号のON、OFFとして出力する。 コンピュータシステムを構成するCPUなどの電子部品は、 様々な論理回路により実現されている。

□ 論理ゲート

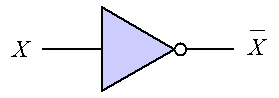
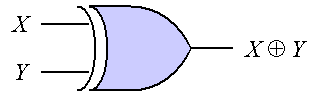
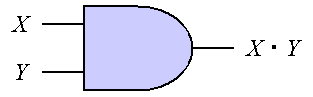
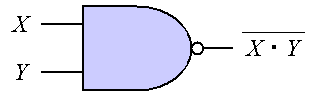
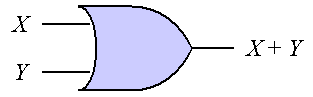
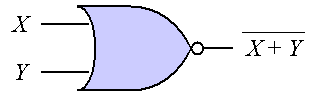
論理回路は、基本的な論理演算を行う 論理ゲート(基本素子)を組み合わせることにより実現される。 命題論理の真偽やブール代数の1、0を電気信号のON、OFFとして入力し、 論理演算を行った結果を電子回路を論理回路と呼ぶ。 論理回路は、基本的な論理演算を行う 論理ゲート(基本素子)を組み合わせることにより実現される。 論理ゲートには、否定(NOT)や論理積(AND)、論理和(OR)に加え、 排他的論理和(XOR)や論理積の否定(NAND)、論理和の否定(NOR)などもある。 各種基本論理ゲートを図1に示す(各ゲートの左が入力で右が出力)。

図1: 各種基本論理ゲート

NOT	XOR
AND	NAND
OR	NOR

ここで初めて出てきた排他的論理和とは、 2つの命題X および命題Y において、 どちらか一方が真の場合のみ真となる論理である。 ブール代数では、二項演算子「⊕ (○の中に+)」により表現され、 その真理値表は表4のようになる。

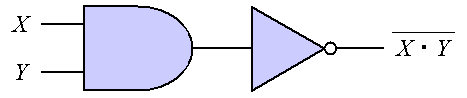
これらの論理ゲートは、それぞれ独立ではなく、 同じ機能を果たす論理回路を他の論理ゲートにより構成することができる。 例えばNANDゲートは、ブール代数で表現すると X ・Y であることから判るように、 図2に示すようにNOTゲートとANDゲートを組み合わせることにより、 同じ機能を果たす論理回路を構成することができる。

図2: NOTゲートとANDゲートによるNAND回路の構成

□ 半加算器と全加算器

CPUをはじめとする情報処理のための各種電子回路は、 基本的に、論理ゲートを組み合わせた論理回路からなる。 例えば、簡単な例として、 1bitの数値X とY の2つを加算し、 2bitの数値を得る演算を行う論理回路は、 演算結果の上位bitをC 、下位bitをS とすると、 図3のように構成することができ、一般に、これを半加算器(Half Adder)と呼ぶ。

図3: 半加算器の論理回路

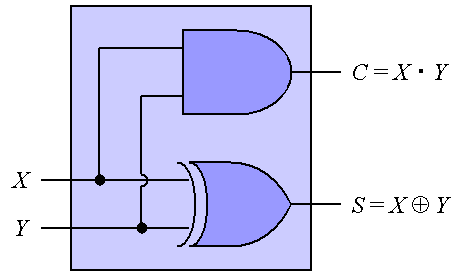この半加算器のC 、S に対する真理値表は、 表5のようになり、確かに1bit同士の数値の加算になることが確認できる。

この半加算器を図4に示すように組み合わせると、 下の桁からの繰り上がりを示すc を考慮した 全加算器を構成することができる。

図4: 全加算器の論理回路

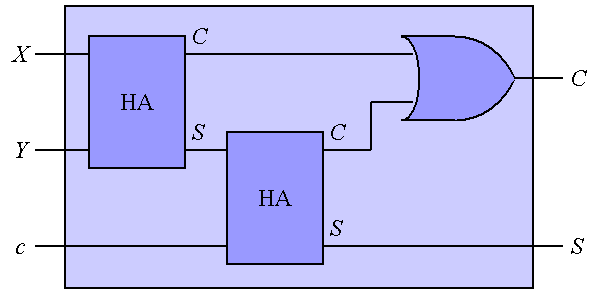この全加算器を複数段組み合わせることにより、 n bitの加算を行う回路を構成できることが容易に想像できる。

レポート課題

■ レポート課題1

問1

排他的論理和(⊕)は、 ブール代数により以下のように定義することができる。

X およびY に対する、 X +Y 、 (X ・Y )、 (X +Y ) ・ (X ・Y ) の真理値表を作成し、 表4で示したX ⊕Y の真理値表と一致することを確認せよ。

問2

命題論理と同様に、ブール代数においても、 任意のX , Y に対してド・モルガンの法則: (X ・ Y ) = X + Y および(X + Y ) = X ・ Y が成り立つことを真理値表を書いて確認せよ。

問3

XおよびYに対する排他的論理和(⊕)は、上記のように表せるほか、 以下のようにも表記できる。

(X +Y ) ・ (X ・Y ) = (X ・Y ) + (X ・Y ) が成り立つことを証明せよ。

■ レポート課題2

一般に、コンピュータのCPUなどを構成するICやLSIでは、 製造が容易なNANDゲートを組み合わせて構成されている。 すなわち、NOT、AND、OR、NOR、XORなどの全ての論理回路を NANDゲートのみの組み合わせにより実現することができる。 例えば、NOTゲートと同じ機能を果たす論理回路が NANDゲートを利用して構成できることは、 NOT演算がブール代数を用いて X = (X・X) のように表記できることからもわかり、 これに基づき図5のように論理回路を構成できる。

図5: NANDゲートによるNOT回路の構成

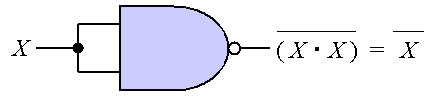これを参考にし、以下の問いに答えよ。

問1

ANDゲートと同じ機能を果たす論理回路をNANDゲートにより構成できることを ブール代数により示せ。 また、ANDゲートと同じ機能の論理回路をNANDゲートにより構成し、図示せよ。

問2

ORゲートと同じ機能をNANDゲートにより構成できることをブール代数により示せ。 また、ORゲートと同じ機能の論理回路をNANDゲートにより構成し、図示せよ。

■ レポート課題3

問1

全加算器は、加算する2つの数値のn 桁目の値X およびY 、 ならびに下の桁からの繰り上がりを示すc の3つの入力に対し、 和を示すS 、および次の桁への繰り上がりを示すC を出力する。 X 、Y 、c の組み合わせに対する S およびC の真理値表を示せ。

ただし、真理値表における入出力の並びは 左からX 、Y 、c 、C 、S の順とし、 その入力値は、上から 0 0 0, 0 0 1, 0 1 0, ... , 1 1 0, 1 1 1 となるように示せ。

表5: 全加算器の真理値表

X	Y	c	C	S
0	0	0
0	0	1
0	1	0
...			...
1	1	0
1	1	1

問2

半加算器と全加算器を組み合わせ、 2bitで表現される数値x およびy を足し合わせ、 (最大)3bitの値z を出力する演算を行なう論理回路を構成し、図示せよ。 このとき、 入力値x の1桁目をX_L 、2桁目をX_H 、 y の1桁目をY_L 、2桁目をY_H 、 演算結果z の1桁目をZ_L 、2桁目をZ_M 、 3桁目をZ_H とし、図中に明記せよ。 また、X_L 、X_H 、 Y_L 、Y_H の入力に対する Z_L 、Z_M 、Z_H の 真理値表を示せ。

ただし、半加算器および全加算器の内部の論理回路を図中に示す必要はないが、 それぞれの論理回路の出力C およびS を 図4の全加算器の論理回路図における半加算器の使用方法と同様に明記せよ。

また、真理値表における入出力の並びは 左からX_H 、X_L 、 Y_H 、Y_L 、 Z_H 、Z_M 、Z_L の順とし (x 、y 、z のそれぞれの上位の桁が左になる)、 その入力値は、上から 0 0 0 0, 0 0 0 1, 0 0 1 0, ... , 1 1 1 0, 1 1 1 1 と なるように示せ。

表5: 2bit同士の加算器の真理値表

XH	XL	YH	YL	ZH	ZM	ZL
0	0	0	0
0	0	0	1
0	0	1	0
...				...
1	1	1	0
1	1	1	1

参考書籍、Web

良さそうな参考文献をまだ探していません...。