2003年度後期 IT教育基礎論演習B
代表的なアルゴリズムとしてソートを例にとり、 手続き型プログラミングによる実装方法を学習する。
一般的なアルゴリズムとデータ構造の1つとして、 配列やリストに格納されたデータ列を順番に並べ替えるソートがある。 ここでは、具体的なソートアルゴリズムの1つであるマージソートの実装方法や、 複合的なデータの扱い、 ライブラリを利用したソートプログラムの記述方法を学習する。
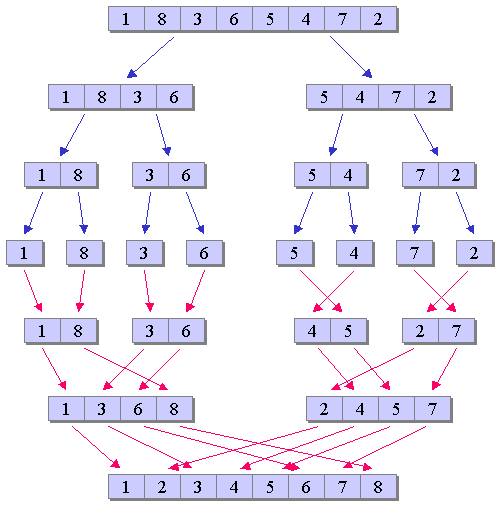
ソートのアルゴリズムとしては、 単純選択法やバブルソート、クイックソート、ヒープソートなど、 多様なアルゴリズムが知られているが、 ここでは、マージソートを例にとり、その実装方法を学習する。 マージソートは、ソートアルゴリズムの1つとしてよく知られたアルゴリズムであり、 分割と統合により定義される。 クイックソート等に比べると効率性に欠ける場合もあるが、 データ列の並び方によらず安定した計算量に収まるといった特徴を持つ。 このマージソートのアルゴリズムは、 ある数列をマージソートによりソートする場合、 一般に、図1のように表される。

|
図1は極めて単純な図であり、 取り立てて複雑なことは行っていないため容易に実装できそうにも思える。 しかしながら実際にプログラムを記述する場合には、 気をつけなければいけない部分も少なくない。
先ず、分割と統合の処理手順に関して、 図1を見ると、先ず、全ての列が要素数1になるまで分割を繰り返し、 その後、統合を繰り返すというような、 上から下に処理が進めればよいように感じられるかもしれない。 しかしながら、マージソートにおける一般的な処理手順は 必ずしも上から下に進められるとは限らない。 マージソートのアルゴリズムは 関数の再帰呼び出しの例として取り上げられることも多く、 一般に、再帰的に以下のように定義することができる。
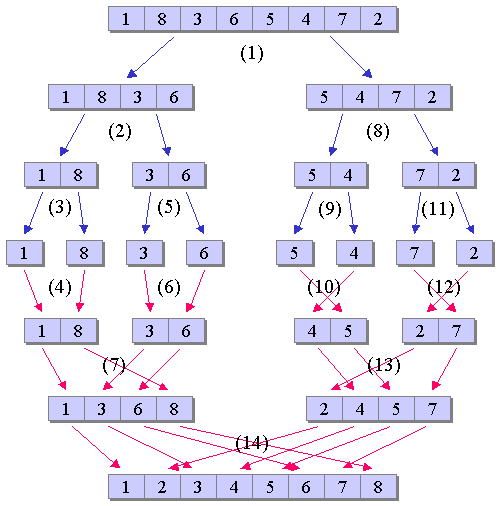
この時、3. の部分が再帰的な定義になっている。 この3.の部分の再帰呼び出しにおいて、 マルチスレッド等の特別な処理を行わず 一般的な逐次処理によりマージソートを行う場合、 例えば、前半部を先にマージソートによりソートし、 これが終了した後に後半部のマージソートを行う、 という形で処理手続きを定義すると、 実際には、前半部のマージソートを行うために、 さらにこれを前半部と後半部に分割し、 さらにまたこの前半部のマージソートを行うために... という具合に処理が進められることになる。 従って、図1のマージソートの例において、 分割、統合の処理に順番に番号をふると、図2のようになる。
|
この図をみるとわかるように、 マージソートによる分割、統合の処理は、 全てを分割した後に統合を行うのではなく、分割と統合を繰り返し、 図の上では、上と下を行きつ戻りつしていることが確認できる。 もし、これを勘違いして、先ず全てを分割しなければならないと思い込んでしまうと、 関数の再帰呼び出しによるプログラムの記述ができなくなってしまう。
配列を前半部と後半部に分割し、 2つの配列とするのにどのようにしたら良いだろうか? 図1では、もともとの数列を2つに分割する際に、 大きさが半分の2つの数列を新たに用意しているように見えるかもしれない。 実際、データ列を分割するたびに新たなデータ列を用意しても プログラムを記述することはできるが、 その場合、分割の段数分だけ新たにデータ列を用意することとなり、 もとのデータの何倍ものデータ格納領域が必要となる。 もし、大量のデータをマージソートによりソートする場合、 これは現実的な方法とはいえない。
これに対し、マージソートにおける分割は、 データ列の入れ替えを行うわけではなく、 処理対象となる範囲を指定しているだけであることに着目すると、 余計なデータ列を生成する必要がないことがわかる。 すなわち、マージソートの手続きを あるデータ列におけるソート範囲の始点と終点を指定するように定義すればよい。 すなわち、マージソートの処理手続きを以下のように定義することができる。
マージソートの処理手続きにおける、 3.の前半部と後半部の2つのデータ列の統合において、 その処理手続きは以下のように定義することができる。
これをそのままプログラムとして実装する方法もあるが、 その場合、統合の処理の度に、 統合済みのデータ列を格納するためデータ格納領域を新たに用意することとなり、 結果的に段数分だけ、新たなデータ格納領域を用意する必要があり、現実的ではない。
これに対し、前半部と後半部の統合のために、それぞれのデータ列を一時的に複製し、 もとのデータ列の格納領域を統合済みデータ列の格納領域として使用すれば、 統合が終了した時点で、 一時的に用意した複製を格納するためのデータ格納領域は使用済みとなり、 次の統合のために新たなデータ格納領域を用意する必要はない。 しかしながら、このような処理手続きの場合にも、 もとのデータ列の大きさと同じだけのデータ格納領域が必要となる。 また、前半部、後半部の統合において、比較による結合の結果残ったデータ列を 必ず統合済みデータ列に結合してやらなければならない。
ここで、2つのデータ列の統合においてデータを1つ1つ結合する度に、 未処理データから1つ1つデータを取り除くことに着目すると、 前半部のみを複製し、退避させてやれば良いことがわかる。 この場合、一時的に用意すべきデータ格納領域は もとのデータ列の半分の大きさで済むだけでなく、 後半部のデータの複製処理、 および比較によるデータ列の結合の結果として後半部のデータ列が残った場合の 未処理データの結合処理を行う必要がなく、 効率的なプログラムの実行が可能となり、大幅な実行速度の向上が見込まれる。
以上のマージソートのアルゴリズムに基づき、 実際に、配列に格納された数列をソートするプログラムを記述すると 以下のようになる。
/* merge-sort-number.c */
#include <stdio.h>
#define ARRAY_MAX 256
/* マージソート関数 array[]: ソート対象配列y, left: 左端, right: 右端 */
void merge_sort(int array[], int left, int right) {
int reserve[ARRAY_MAX / 2 + 1]; /* 前半部退避用の配列 */
int mid; /* 左端と右端の中間位置を示す変数 */
int i; /* 退避用配列の添え字のカウンタ */
int reserve_end; /* 退避用配列の右端 */
int j; /* ソート対象配列の後半部の添え字のカウンタ */
int k; /* ソート対象配列の添え字のカウンタ */
if ( left == right ) return; /* 配列の要素が空であれば何もせず戻る */
mid = (left + right) / 2; /* 配列の中間位置を求める */
merge_sort(array, left, mid); /* 再帰呼び出しにより前半部をソート */
merge_sort(array, mid + 1, right); /* 再帰呼び出しにより後半部をソート */
for( i = 0, k = left; k <= mid; i++, k++ ) { /* 前半部を退避 */
reserve[i] = array[k];
}
i = 0; /* 退避された前半部の比較位置の初期値を設定 */
j = mid + 1; /* 後半部の比較位置の初期値を設定 */
reserve_end = mid - left; /* 退避された前半部の右端を設定 */
k = left; /* マージした結果の格納位置の初期値を設定 */
/* 退避された前半部、および後半部が残っている間、マージ */
while( i <= reserve_end && j <= right ) {
if ( reserve[i] <= array[j] ) {
array[k] = reserve[i]; /* 退避された前半部からマージ */
i++;
} else {
array[k] = array[j]; /* 後半部からマージ */
j++;
}
k++; /* マージ位置を右に移動 */
}
/* 比較によるマージ後、退避された前半部が残っていれば無条件にマージ */
while( i <= reserve_end ) {
array[k] = reserve[i];
i++;
k++;
}
}
int main(int argc, char **argv) {
int array[ARRAY_MAX] = { 1, 8, 3, 6, 5, 4, 7, 2 }; /* ソート対象配列 */
int i;
merge_sort(array, 0, 7); /* マージソート関数呼び出し */
for( i = 0; i < 8; i++ ) { /* 結果出力 */
printf("%d ", array[i] );
}
printf("\n");
}
|
このプログラムを実行すると、 以下のように正しくソートすることができることを確認できる。
./merge-sort-number 1 2 3 4 5 6 7 8 |
整数など、データの大きさが小さいデータを要素とするデータ列のソートでは、 その要素そのものを移動させることによりソートを行うが、 文字配列や構造体など、複数のデータからなる複合的なデータを 1つの要素とするデータ列のソートを行う場合に、 その要素自身を移動させていると、そのための処理に時間がかかってしまう。 また、文字配列のように、もし、その大きさが不特定のデータを扱う場合には、 ソートの途中やソートの結果、どこにどのデータが格納されるかわからないため、 各要素を格納するためのデータ領域として、 データ列の中で最も大きなデータを格納できる十分な大きさのデータ格納領域を 用意する必要が生じ、効率的ではない。
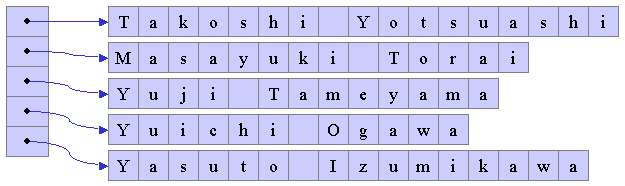
このような複合的なデータや、大きさの不確定な大きなデータのソートを行う場合、 データ自身の並び替えを行うのではなく、 データを格納してる場所を示すデータ列を用意し、 このデータ列を並び替えを行うとよい。 例えば、文字列の並び替えを行いたい場合、 C言語では、図3に示すように文字配列へのポインタを示すデータ列を格納する 配列を用意する。
|
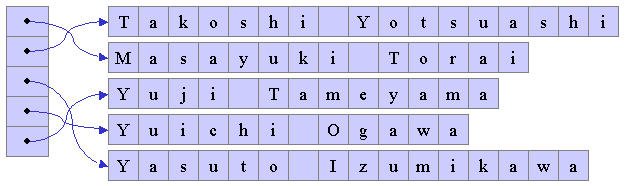
このポインタの配列の要素を対応する文字配列の内容に従ってソートすることにより、 図4に示すように、実質的に文字列を順番に並べたのと同等となる。
|
このように、ポインタのソートによる文字列の並び替えを マージソートにより行うプログラムは、以下のように記述することができる。
/* merge-sort-string.c */
#include <stdio.h>
#include <string.h>
#define ARRAY_MAX 256
/* マージソート関数 array[]: ソート対象配列y, left: 左端, right: 右端 */
void merge_sort(char **array, int left, int right) {
char *reserve[ARRAY_MAX / 2 + 1]; /* 前半部退避用の配列 */
int mid; /* 左端と右端の中間位置を示す変数 */
int i; /* 退避用配列の添え字のカウンタ */
int reserve_end; /* 退避用配列の右端 */
int j; /* ソート対象配列の後半部の添え字のカウンタ */
int k; /* ソート対象配列の添え字のカウンタ */
if ( left == right ) return; /* 配列の要素が空であれば何もせず戻る */
mid = (left + right) / 2; /* 配列の中間位置を求める */
merge_sort(array, left, mid); /* 再帰呼び出しにより前半部をソート */
merge_sort(array, mid + 1, right); /* 再帰呼び出しにより後半部をソート */
for( i = 0, k = left; k <= mid; i++, k++ ) { /* 前半部を退避 */
reserve[i] = array[k];
}
i = 0; /* 退避された前半部の比較位置の初期値を設定 */
j = mid + 1; /* 後半部の比較位置の初期値を設定 */
reserve_end = mid - left; /* 退避された前半部の右端を設定 */
k = left; /* マージした結果の格納位置の初期値を設定 */
/* 退避された前半部、および後半部が残っている間、マージ */
while( i <= reserve_end && j <= right ) {
if ( strcmp(reserve[i], array[j]) < 0 ) {
array[k] = reserve[i]; /* 退避された前半部からマージ */
i++;
} else {
array[k] = array[j]; /* 後半部からマージ */
j++;
}
k++; /* マージ位置を右に移動 */
}
/* 比較によるマージ後、退避された前半部が残っていれば無条件にマージ */
while( i <= reserve_end ) {
array[k] = reserve[i];
i++;
k++;
}
}
int main(int argc, char **argv) {
char *array[ARRAY_MAX] /* ソート対象配列 */
= { "Eiji MURAMOTO",
"Takoshi YOTSUASHI",
"Shinji WATABE",
"Masayuki TORAI",
"Yuji TAMEYAMA",
"Ryuichi WATANABE",
"Shin KAWASAKI",
"Yuichi OGAWA",
"Toshiro OGIWARA",
"Katsuro KITAMACHI",
"Yasuto IZUMIKAWA" };
int i;
merge_sort(array, 0, 10); /* マージソート関数呼び出し */
for( i = 0; i < 11; i++ ) { /* 結果出力 */
printf("%s\n", array[i] );
}
}
|
このプログラムの実行結果は以下のようになり、 ただしく文字列のソートを行えることが確認できる。
$ ./merge-sort-string Eiji MURAMOTO Katsuro KITAMACHI Masayuki TORAI Ryuichi WATANABE Shin KAWASAKI Shinji WATABE Takoshi YOTSUASHI Toshiro OGIWARA Yasuto IZUMIKAWA Yuichi OGAWA Yuji TAMEYAMA |
データ列のソートは、様々なプログラムで利用されることが多い。 そのため、C言語では、 stdlibで宣言されている標準Cライブラリに、 データ列をクイックソートと呼ばれるアルゴリズムによりソートを行う qsort()関数が用意されている。 qsort()関数では、 配列に格納されたデータ列の要素を指定された条件により比較し、ソートする。 そのために、引数として、ソート対象となる配列へのポインタ、 その配列の要素数、各要素の大きさ、 および要素間の比較のための関数へのポインタを指定する必要があり、 その仕様は以下のようになっている。
| 関数名 | 戻り値 | 引数1 | 引数2 | 引数3 | 引数4 | qsort | なし | 配列へのポインタ | 配列の大きさ | 要素の大きさ | 関数へのポインタ |
|---|
このとき、多様なデータ列を対象とするために、 引数として与えられる配列へのポインタは、 型のない配列(void型の配列)へのポインタとなっており、 配列の要素数、ならびに各要素の大きさは、 データの大きさを示す汎用的なsize_t型となっている。 従って、qsort()関数へこれらの値を渡す際に、 指定された型への変換を行う必要がある。 データの大きさを得るには、 指定されえた型の大きさを求めるマクロである sizeof()マクロを利用すると便利である。
関数へのポインタとは、 一般のポインタがデータの格納領域を示しているのと同様に、 関数の実体が格納されている場所を示すものであり、 function()という関数であれば、 ポインタ変数functionを参照することにより、 その関数へのポインタを得ることができる。 このとき、qsort()関数で利用する比較を行うための関数は、 配列の2つの要素への型のないポインタを引数としてとり、 戻り値として第1引数で指定されたポインタの示す値が 第2引数で指定されたポインタの示す値よりも 小さいとみなす場合は負、 第1引数で指定されたポインタの示す値が 第2引数で指定されたポインタの示す値よりも 大きいとみなす場合は正、 第1引数で指定されたポインタの示す値と 第2引数で指定されたポインタの示す値が等しいとみなす場合は 0のint型の値を返す形で定義する必要がある。 また、関数の中で引数として渡されたポインタを利用する場合には、 そのポインタの型がないため、適宜、型変換する必要もある。
例えば、qsort()関数の仕様に基づき、 配列に格納された整数をソートするプログラムは以下のように記述することができる。
/* quick-sort-number.c */
#include <stdio.h>
#include <stdlib.h>
#define ARRAY_MAX 256
/* 整数の大小を比較するための関数の定義 */
int compare_number(const void *a, const void *b) {
int i, j;
i = *((int *)a);
j = *((int *)b);
if ( i < j ) return -1;
else if ( i > j ) return 1;
return 0;
}
int main(int argc, char **argv) {
int array[] = { 1, 8, 3, 6, 5, 4, 7, 2 }; /* ソート対象配列 */
int i;
qsort((void *)array, (size_t)8, (size_t)sizeof(int), compare_number); /* qsort()関数呼び出し */
for( i = 0; i < 8; i++ ) { /* 結果出力 */
printf("%d ", array[i] );
}
printf("\n");
}
|
同様に、文字配列へのポインタの配列をqsort()関数により ソートするプログラムは以下のように記述することができる。
/* quick-sort-string.c */
#include <stdio.h>
#include <stdlib.h>
#define ARRAY_MAX 256
/* 文字列の大小を比較するための関数の定義 */
int compare_string(const void *a, const void *b) {
char *s, *t;
s = (char *)*(char **)a;
t = (char *)*(char **)b;
return strcmp(s, t);
}
int main(int argc, char **argv) {
char *array[ARRAY_MAX] /* ソート対象配列 */
= { "Eiji MURAMOTO",
"Takoshi YOTSUASHI",
"Shinji WATABE",
"Masayuki TORAI",
"Yuji TAMEYAMA",
"Ryuichi WATANABE",
"Shin KAWASAKI",
"Yuichi OGAWA",
"Toshiro OGIWARA",
"Katsuro KITAMACHI",
"Yasuto IZUMIKAWA" };
int i;
qsort((void *)array, (size_t)11, (size_t)sizeof(char *), compare_string); /* qsort()関数呼び出し */
for( i = 0; i < 11; i++ ) { /* 結果出力 */
printf("%s\n", array[i] );
}
}
|
このように、予めライブラリで用意されているソート関数を利用することにより、 大小比較のための関数定義が多少煩わしいもののソートの手続きをいちいち プログラムに記述する必要がなく、プログラムを容易に記述することができる。
学籍番号(文字列)、氏名(ローマ字で名前、苗字の順の文字列)、 性別(整数: 0ならば女性、1ならば男性とする)、 年齢(整数)からなる構造体を利用し、 標準入力から入力された学生名簿の一覧を 氏名がアルファベット順になるようにマージソートによりソートし、 各学生ごとに学籍番号、氏名、性別(maleもしくはfemale)、年齢を 標準出力に出力するプログラムを作成せよ。
標準入力から入力された 学籍番号(文字列)、氏名(ローマ字で名前、苗字の順の文字列)、 性別(整数: 0ならば女性、1ならば男性とする)、 年齢(整数)からなる学生名簿において、 学籍番号順、氏名のアルファベット順、年齢順のいずれかを選択すると、 指定された順序による一覧を標準出力に出力するプログラムを qsort()関数を利用して作成せよ。